Η δύναμη στο ελατήριο στη διάρκεια μιας αατ
Ένα σώμα μάζας m, είναι δεμένο στο κάτω άκρο ιδανικού ελατηρίου και συγκρατείται στην θέση (1) όπου το ελατήριο έχει το φυσικό μήκος του ℓ0. Σε μια στιγμή t=0 αφήνουμε το σώμα οπότε εκτελεί αατ.
Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες:
i) Η δύναμη που το σώμα ασκεί στο ελατήριο, μόλις αφεθεί να κινηθεί, είναι ίση με το βάρος w=mg.
ii) Η μέγιστη δύναμη που το σώμα ασκεί στο ελατήριο είναι διπλάσια του βάρους w.
iii) Η μέγιστη δυναμική ενέργεια του ελατηρίου είναι τετραπλάσια της ενέργειας ταλάντωσης.
Να δικαιολογήσετε τις απαντήσεις σας.
Απάντηση: ή
Η δύναμη στο ελατήριο στη διάρκεια μιας αατ
Η δύναμη στο ελατήριο στη διάρκεια μιας αατ
Παρεμβάλλοντας μια αντλία.
Σε ένα οριζόντιο σωλήνα σταθερής διατομής, έχουμε σταθερή ταχύτητα ροής υ1.
«Αν θέλουμε να αυξήσουμε την παροχή του σωλήνα, μπορούμε να παρεμβάλουμε μια αντλία, όπως στο κάτω σχήμα, οπότε το νερό θα φτάνει σε αυτήν με ταχύτητα ροής υ1, θα παίρνει ενέργεια από την αντλία και θα συνεχίζει με ταχύτητα υ2.»
Συμφωνείτε ή διαφωνείτε με την παραπάνω πρόταση;
Οι ροές να θεωρηθούν μόνιμες ροές ιδανικού ρευστού.
Απάντηση: ή
Παρεμβάλλοντας μια αντλία.
Παρεμβάλλοντας μια αντλία.
Μια διπλή ισορροπία ενός αγωγού
Ο αγωγός ΑΓ αφήνεται ελεύθερος σε επαφή με δύο κατακόρυφους στύλους, οι οποίο δεν παρουσιάζουν αντίσταση και στα πάνω άκρα τους συνδέεται μια πηγή Ε, ενώ στα κάτω άκρα τους συνδέεται με ανοικτό διακόπτη δ, ένας αντιστάτης με αντίσταση R. Ο αγωγός ΑΓ ισορροπεί, ενώ στην περιοχή υπάρχει ένα οριζόντιο ομογενές μαγνητικό επίπεδο με δυναμικές γραμμές κάθετες στο επίπεδο του σχήματος.
i) Να σχεδιάσετε την ένταση του μαγνητικού πεδίου που υπάρχει στο χώρο.
ii) Σε μια στιγμή κλείνουμε το διακόπτη δ και παρατηρούμε ότι ο αγωγός ΑΓ συνεχίζει να ισορροπεί. Με δεδομένο ότι η επίδραση των μαγνητικών πεδίων των υπολοίπων αγωγών στον ΑΓ θεωρείται αμελητέα, για την εσωτερική αντίσταση της πηγής, ισχύει:
α) r=0, β) r= ½ R, γ) r =R.
Να δικαιολογήσετε τις απαντήσεις σας, θεωρώντας ότι ο αγωγός ΑΓ έχει αντίσταση RΑΓ.
Απάντηση: ή
Μια διπλή ισορροπία ενός αγωγού
Μια διπλή ισορροπία ενός αγωγού
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
Ένα σώμα Α που κινείται σε λείο οριζόντιο επίπεδο, συγκρούεται κεντρικά και ελαστικά κάποια στιγμή με ένα δεύτερο σώμα Β. Στο σχήμα δίνεται το διάγραμμα της ορμής του σώματος Α σε συνάρτηση με το χρόνο.
i) Να εξηγήσετε γιατί το σώμα Β πριν την κρούση κινείται και να βρείτε την φορά της κίνησής του.
ii) Ποιο από τα παρακάτω διαγράμματα, τα οποία εμφανίζουν την μεταβολή της ορμής του Β σώματος σε συνάρτηση με το χρόνο, μπορεί να είναι σωστό;
Απάντηση. ή
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
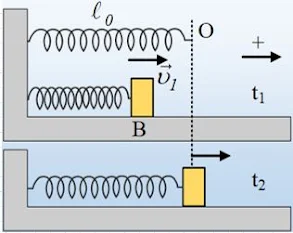
Το σώμα του σχήματος, αμελητέων διαστάσεων, ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου και τη στιγμή t1 περνά από την θέση Β, με ταχύτητα υ1 με κατεύθυνση προς τα δεξιά. Στο σώμα ασκείται δύναμη απόσβεσης Fαπ=-bυ και η κίνηση μπορεί να είναι φθίνουσα ή και εξαναγκασμένη, αφού μπορεί να ασκείται στο σώμα και εξωτερική αρμονική δύναμη.
i) Η θέση ισορροπίας, από την οποία μετράμε και την απομάκρυνση x, είναι η θέση Ο, όπου το ελατήριο έχει το φυσικό μήκος του:
Α) Μόνο για την περίπτωση της φθίνουσας ταλάντωσης.
Β) Μόνο για την εξαναγκασμένη ταλάντωση.
Γ) Και στις δύο ταλαντώσεις.
Δ) Σε καμιά από τις δύο αυτές ταλαντώσεις.
ii) Αν η ταλάντωση είναι φθίνουσα:
Α) Η επιτάχυνση του σώματος στη θέση Β, όπου η απομάκρυνση είναι x1, έχει μέτρο:
α) α1< k|x1|/m, β) α1= k|x1|/m, γ) α1> k|x1|/m.
Β) Η επιτάχυνση του σώματος στη θέση Ο είναι μηδενική ή όχι;
Γ) Το σώμα θα ξαναπεράσει από την θέση Β κινούμενο προς τα δεξιά, μια επόμενη χρονική στιγμή t3, έχοντας ενέργεια ταλάντωσης Ε3 και επιτάχυνση μέτρου α3.
Γ1) Αν η ενέργεια ταλάντωσης την στιγμή t1 είναι ίση με Ε1, τότε:
α) Ε3 < Ε1, β) Ε3 = Ε1, γ) Ε3 > Ε1.
Γ2) Για τα μέτρα των επιταχύνσεων α1 και α3 ισχύει:
α) α3 < α1, β) α3 = α1, γ) α3 > α1.
iii) Αν η ταλάντωση του σώματος είναι εξαναγκασμένη και η απομάκρυνση του σώματος ικανοποιεί την εξίσωση x=Α∙ημ(ωδt):
Α) Η επιτάχυνση του σώματος στη θέση Ο είναι μηδενική ή όχι;
Β) Αν το σώμα τη στιγμή t1 έχει επιτάχυνση α1 και ενέργεια ταλάντωσης Ε1, τότε όταν το σώμα θα ξαναπεράσει από την θέση Β κινούμενο προς τα δεξιά, μια επόμενη χρονική στιγμή t3, έχοντας ενέργεια Ε3 και επιτάχυνση μέτρου α3, θα ισχύουν:
Β1) Για τις ενέργειες ταλάντωσης:
α) Ε3 < Ε1, β) Ε3 = Ε1, γ) Ε3 > Ε1.
Β2) Για τα μέτρα των επιταχύνσεων α1 και α3 ισχύει:
α) α3 < α1, β) α3 = α1, γ) α3 > α1.
Να δικαιολογήσετε τις απαντήσεις σας.
Απάντηση: ή
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
Μια θέση σε μια εξαναγκασμένη ταλάντωση
Ένα σώμα εκτελεί εξαναγκασμένη ταλάντωση δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου, γύρω από την θέση ισορροπίας Ο, σε λείο οριζόντιο επίπεδο με την επίδραση αρμονικής εξωτερικής δύναμης Fδ. Στο σχήμα δίνονται 4 θέσεις με σημειωμένες τις ταχύτητες του σώματος. Σε μια από τις θέσεις αυτές η δύναμη του ελατηρίου είναι αντίθετη της δύναμης απόσβεσης (Fελ=-Fαπ).
i) Σε ποια από τις θέσεις του σχήματος βρίσκεται το σώμα.
iii) Να σχεδιάσετε τις δυνάμεις που ασκούνται στο σώμα στην θέση που θα επιλέξετε.
Να δικαιολογήσετε τις απαντήσεις σας.
Απάντηση: ή
Μια θέση σε μια εξαναγκασμένη ταλάντωση
Μια θέση σε μια εξαναγκασμένη ταλάντωση
Ένα σώμα μάζας m, είναι δεμένο στο κάτω άκρο ιδανικού ελατηρίου και συγκρατείται στην θέση (1) όπου το ελατήριο έχει το φυσικό μήκος του ℓ0. Σε μια στιγμή t=0 αφήνουμε το σώμα οπότε εκτελεί αατ.
Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες:
i) Η δύναμη που το σώμα ασκεί στο ελατήριο, μόλις αφεθεί να κινηθεί, είναι ίση με το βάρος w=mg.
ii) Η μέγιστη δύναμη που το σώμα ασκεί στο ελατήριο είναι διπλάσια του βάρους w.
iii) Η μέγιστη δυναμική ενέργεια του ελατηρίου είναι τετραπλάσια της ενέργειας ταλάντωσης.
Να δικαιολογήσετε τις απαντήσεις σας.
Απάντηση: ή
Η δύναμη στο ελατήριο στη διάρκεια μιας αατ
Η δύναμη στο ελατήριο στη διάρκεια μιας αατ
Παρεμβάλλοντας μια αντλία.
«Αν θέλουμε να αυξήσουμε την παροχή του σωλήνα, μπορούμε να παρεμβάλουμε μια αντλία, όπως στο κάτω σχήμα, οπότε το νερό θα φτάνει σε αυτήν με ταχύτητα ροής υ1, θα παίρνει ενέργεια από την αντλία και θα συνεχίζει με ταχύτητα υ2.»
Συμφωνείτε ή διαφωνείτε με την παραπάνω πρόταση;
Οι ροές να θεωρηθούν μόνιμες ροές ιδανικού ρευστού.
Απάντηση: ή
Παρεμβάλλοντας μια αντλία.
Παρεμβάλλοντας μια αντλία.
Μια διπλή ισορροπία ενός αγωγού
i) Να σχεδιάσετε την ένταση του μαγνητικού πεδίου που υπάρχει στο χώρο.
ii) Σε μια στιγμή κλείνουμε το διακόπτη δ και παρατηρούμε ότι ο αγωγός ΑΓ συνεχίζει να ισορροπεί. Με δεδομένο ότι η επίδραση των μαγνητικών πεδίων των υπολοίπων αγωγών στον ΑΓ θεωρείται αμελητέα, για την εσωτερική αντίσταση της πηγής, ισχύει:
α) r=0, β) r= ½ R, γ) r =R.
Να δικαιολογήσετε τις απαντήσεις σας, θεωρώντας ότι ο αγωγός ΑΓ έχει αντίσταση RΑΓ.
Απάντηση: ή
Μια διπλή ισορροπία ενός αγωγού
Μια διπλή ισορροπία ενός αγωγού
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
i) Να εξηγήσετε γιατί το σώμα Β πριν την κρούση κινείται και να βρείτε την φορά της κίνησής του.
ii) Ποιο από τα παρακάτω διαγράμματα, τα οποία εμφανίζουν την μεταβολή της ορμής του Β σώματος σε συνάρτηση με το χρόνο, μπορεί να είναι σωστό;
Απάντηση. ή
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
Το νερό σε τρεις κατακόρυφους σωλήνες
Στο σχήμα βλέπετε έναν λεπτό οριζόντιο κυλινδρικό σωλήνα σταθερής διατομής, ο οποίος συνδέεται κοντά στον πυθμένα ενός πολύ μεγάλου ανοικτού δοχείου με νερό. Ο σωλήνας κλείνεται στο δεξιό άκρο του με τάπα, ενώ πάνω του έχουν προσαρμοσθεί τρεις λεπτοί κατακόρυφοι σωλήνες. Ο Α είναι κλειστός και γεμάτος πλήρως με νερό μέχρι ύψος h=1m, ο Β είναι ανοικτός και το νερό έχει ανέβη επίσης κατά h, ενώ ο Γ στο κάτω άκρο του σχηματίζει μια γωνία, όπως εμφανίζεται στο σχήμα, καταλήγοντας σε οριζόντιο μικρό άνοιγμα και στον οποίο το νερό έχει ανέβη επίσης σε ύψος h.
1) Ποιο το ύψος του νερού μέσα στο δοχείο; (στο σχήμα τα τοιχώματά του είναι αδιαφανή και δεν βλέπουμε το νερό…)
2) Σε μια στιγμή ανοίγουμε την τάπα, οπότε το νερό αρχίζει να εκρέει στην ατμόσφαιρα. Αμέσως μετά την αποκατάσταση μόνιμης ροής:
Γνωρίζοντας την ισχύ της αντλίας
Μια αντλία, με την βοήθεια σωλήνα σταθερής διατομής, αντλεί νερό από δεξαμενή δουλεύοντας με ισχύ Ρα=3gh(dm/dt), h η κατακόρυφη απόσταση μεταξύ του άκρου εκροής του σωλήνα (σημείο Δ) και της επιφάνειας του νερού στη δεξαμενή (σημείο Β), αλλά και το βάθος που βυθίζεται κατακόρυφα ο σωλήνας στο νερό και dm/dt ο ρυθμός με τον οποίο μεταφέρεται η μάζα του νερού. Η ροή θεωρείται μόνιμη ροή ιδανικού ρευστού.
i) Η ταχύτητα εκροής του νερού, έχει μέτρο:
ii) Η πίεση στο σημείο Β (στο εσωτερικό του σωλήνα στο επίπεδο της ελεύθερης επιφάνειας), είναι ίση:
α) pΒ < pατμ, β) pΒ = pατμ, γ) pΒ > pατμ.
iii) Η πίεση στο σημείο Α (στο εσωτερικό του σωλήνα, στο κάτω άκρο του ) είναι ίση:
α) pΑ = pατμ+ρgh β) pΑ = pΒ+ ρgh γ) pΑ > pατμ+ρgh.
Απάντηση: ή
Γνωρίζοντας την ισχύ της αντλίας
Γνωρίζοντας την ισχύ της αντλίας
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
Μια κεντρική ελαστική κρούση και ένα διάγραμμα
Το νερό σε τρεις κατακόρυφους σωλήνες
1) Ποιο το ύψος του νερού μέσα στο δοχείο; (στο σχήμα τα τοιχώματά του είναι αδιαφανή και δεν βλέπουμε το νερό…)
2) Σε μια στιγμή ανοίγουμε την τάπα, οπότε το νερό αρχίζει να εκρέει στην ατμόσφαιρα. Αμέσως μετά την αποκατάσταση μόνιμης ροής:
i) Το νερό στον Α σωλήνα έχει ανέβη σε ύψος h1, όπου:
α) h1 =0, β) h1 < h , γ) h1 =h.
ii) Το νερό στον Β σωλήνα έχει ανέβη σε ύψος h2, όπου:
α) h2 =0, β) h2 < h , γ) h2 =h.
iii) Το νερό στον Γ σωλήνα έχει ανέβη σε ύψος h3, όπου:
α) h3 =0, β) h3 < h , γ) h3 =h.
Υπενθυμίζεται ότι το νερό μπορεί να φτάσει σε ύψος 10m, σε κλειστό σωλήνα, ο οποίος είναι κενός.
Απάντηση: ή
Το νερό σε τρεις κατακόρυφους σωλήνες
Το νερό σε τρεις κατακόρυφους σωλήνες
Ο μαγνήτης πλησιάζει ένα κυκλικό πλαίσιο
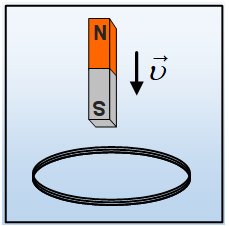Ένας ραβδόμορφος μαγνήτης πέφτει κατακόρυφα, πλησιάζοντας ένα σταθερό οριζόντιο κυκλικό πλαίσιο, το οποίο αποτελείται από ν κυκλικούς αγωγούς, σχηματίζοντας κλειστό κύκλωμα. Τη στιγμή t1 που δείχνει το διπλανό σχήμα, η δυναμική ενέργεια του μαγνήτη μειώνεται κατά 6J/s.
i) Να εξηγήσετε γιατί το πλαίσιο διαρρέεται από ρεύμα και να βρείτε την φορά του για την στιγμή t1 του σχήματος.
ii) Την στιγμή t1 η κινητική ενέργεια του μαγνήτη αυξάνεται με ρυθμό:
α) 5J/s, β) 6J/s, γ) 7J/s.
Να δικαιολογήσετε τις απαντήσεις σας.
Η αντίσταση του αέρα θεωρείται αμελητέα.
Απάντηση: ή
Ο μαγνήτης πλησιάζει ένα κυκλικό πλαίσιο
Ο μαγνήτης πλησιάζει ένα κυκλικό πλαίσιο
Μια πλαστική κρούση εν μέσω αατ.
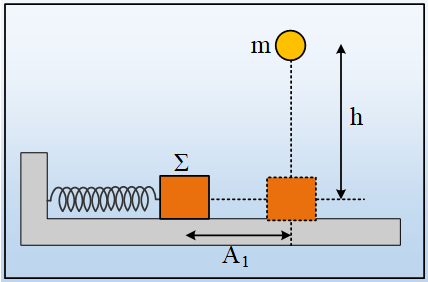Ένα σώμα Σ, μάζας Μ, είναι δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k και μπορεί να εκτελεί ΑΑΤ σε λείο οριζόντιο επίπεδο. Εκτρέπουμε το σώμα Σ από τη θέση ισορροπίας του και σε μια στιγμή t=0 το αφήνουμε να ταλαντωθεί, ενώ ταυτόχρονα από ύψος h αφήνουμε μια σφαίρα μάζας m=7Μ/9, να πέσει. Ακολουθεί πλαστική κρούση του σώματος Σ με την σφαίρα, τη στιγμή που το σώμα Σ περνά από την θέση ισορροπίας του για πρώτη φορά, χωρίς το συσσωμάτωμα να αναπηδά.
i) Αν Α1 το πλάτος της ταλάντωσης πριν την κρούση και Α2 το πλάτος ταλάντωσης του συσσωματώματος, μετά την κρούση, ισχύει:
α) Α2=0,25 Α1, β) Α2=0,5 Α1, γ) Α2=0,75 Α1.
ii) Η σφαίρα αφέθηκε να πέσει από ύψος h ίσο με:
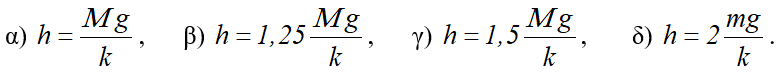
Δίνεται π2≈10, ενώ τη στιγμή της κρούσης το σώμα Σ περνά για πρώτη φορά από τη θέση ισορροπίας.
Απάντηση: ή
Μια πλαστική κρούση εν μέσω αατ.
Μια πλαστική κρούση εν μέσω αατ.
α) h1 =0, β) h1 < h , γ) h1 =h.
ii) Το νερό στον Β σωλήνα έχει ανέβη σε ύψος h2, όπου:
α) h2 =0, β) h2 < h , γ) h2 =h.
iii) Το νερό στον Γ σωλήνα έχει ανέβη σε ύψος h3, όπου:
α) h3 =0, β) h3 < h , γ) h3 =h.
Υπενθυμίζεται ότι το νερό μπορεί να φτάσει σε ύψος 10m, σε κλειστό σωλήνα, ο οποίος είναι κενός.
Απάντηση: ή
Το νερό σε τρεις κατακόρυφους σωλήνες
Το νερό σε τρεις κατακόρυφους σωλήνες
Ο μαγνήτης πλησιάζει ένα κυκλικό πλαίσιο
i) Να εξηγήσετε γιατί το πλαίσιο διαρρέεται από ρεύμα και να βρείτε την φορά του για την στιγμή t1 του σχήματος.
ii) Την στιγμή t1 η κινητική ενέργεια του μαγνήτη αυξάνεται με ρυθμό:
α) 5J/s, β) 6J/s, γ) 7J/s.
Να δικαιολογήσετε τις απαντήσεις σας.
Η αντίσταση του αέρα θεωρείται αμελητέα.
Απάντηση: ή
Ο μαγνήτης πλησιάζει ένα κυκλικό πλαίσιο
Ο μαγνήτης πλησιάζει ένα κυκλικό πλαίσιο
Μια πλαστική κρούση εν μέσω αατ.
i) Αν Α1 το πλάτος της ταλάντωσης πριν την κρούση και Α2 το πλάτος ταλάντωσης του συσσωματώματος, μετά την κρούση, ισχύει:
α) Α2=0,25 Α1, β) Α2=0,5 Α1, γ) Α2=0,75 Α1.
ii) Η σφαίρα αφέθηκε να πέσει από ύψος h ίσο με:
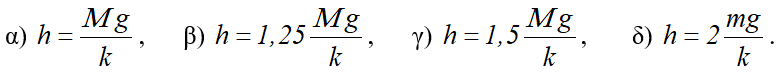
Δίνεται π2≈10, ενώ τη στιγμή της κρούσης το σώμα Σ περνά για πρώτη φορά από τη θέση ισορροπίας.
Απάντηση: ή
Μια πλαστική κρούση εν μέσω αατ.
Μια πλαστική κρούση εν μέσω αατ.
Γνωρίζοντας την ισχύ της αντλίας
i) Η ταχύτητα εκροής του νερού, έχει μέτρο:
ii) Η πίεση στο σημείο Β (στο εσωτερικό του σωλήνα στο επίπεδο της ελεύθερης επιφάνειας), είναι ίση:
α) pΒ < pατμ, β) pΒ = pατμ, γ) pΒ > pατμ.
iii) Η πίεση στο σημείο Α (στο εσωτερικό του σωλήνα, στο κάτω άκρο του ) είναι ίση:
α) pΑ = pατμ+ρgh β) pΑ = pΒ+ ρgh γ) pΑ > pατμ+ρgh.
Απάντηση: ή
Γνωρίζοντας την ισχύ της αντλίας
Γνωρίζοντας την ισχύ της αντλίας
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
i) Η θέση ισορροπίας, από την οποία μετράμε και την απομάκρυνση x, είναι η θέση Ο, όπου το ελατήριο έχει το φυσικό μήκος του:
Α) Μόνο για την περίπτωση της φθίνουσας ταλάντωσης.
Β) Μόνο για την εξαναγκασμένη ταλάντωση.
Γ) Και στις δύο ταλαντώσεις.
Δ) Σε καμιά από τις δύο αυτές ταλαντώσεις.
ii) Αν η ταλάντωση είναι φθίνουσα:
Α) Η επιτάχυνση του σώματος στη θέση Β, όπου η απομάκρυνση είναι x1, έχει μέτρο:
α) α1< k|x1|/m, β) α1= k|x1|/m, γ) α1> k|x1|/m.
Β) Η επιτάχυνση του σώματος στη θέση Ο είναι μηδενική ή όχι;
Γ) Το σώμα θα ξαναπεράσει από την θέση Β κινούμενο προς τα δεξιά, μια επόμενη χρονική στιγμή t3, έχοντας ενέργεια ταλάντωσης Ε3 και επιτάχυνση μέτρου α3.
Γ1) Αν η ενέργεια ταλάντωσης την στιγμή t1 είναι ίση με Ε1, τότε:
α) Ε3 < Ε1, β) Ε3 = Ε1, γ) Ε3 > Ε1.
Γ2) Για τα μέτρα των επιταχύνσεων α1 και α3 ισχύει:
α) α3 < α1, β) α3 = α1, γ) α3 > α1.
iii) Αν η ταλάντωση του σώματος είναι εξαναγκασμένη και η απομάκρυνση του σώματος ικανοποιεί την εξίσωση x=Α∙ημ(ωδt):
Α) Η επιτάχυνση του σώματος στη θέση Ο είναι μηδενική ή όχι;
Β) Αν το σώμα τη στιγμή t1 έχει επιτάχυνση α1 και ενέργεια ταλάντωσης Ε1, τότε όταν το σώμα θα ξαναπεράσει από την θέση Β κινούμενο προς τα δεξιά, μια επόμενη χρονική στιγμή t3, έχοντας ενέργεια Ε3 και επιτάχυνση μέτρου α3, θα ισχύουν:
Β1) Για τις ενέργειες ταλάντωσης:
α) Ε3 < Ε1, β) Ε3 = Ε1, γ) Ε3 > Ε1.
Β2) Για τα μέτρα των επιταχύνσεων α1 και α3 ισχύει:
α) α3 < α1, β) α3 = α1, γ) α3 > α1.
Να δικαιολογήσετε τις απαντήσεις σας.
Απάντηση: ή
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
Μια θέση σε μια εξαναγκασμένη ταλάντωση
i) Σε ποια από τις θέσεις του σχήματος βρίσκεται το σώμα.
iii) Να σχεδιάσετε τις δυνάμεις που ασκούνται στο σώμα στην θέση που θα επιλέξετε.
Να δικαιολογήσετε τις απαντήσεις σας.
Απάντηση: ή
Μια θέση σε μια εξαναγκασμένη ταλάντωση
Μια θέση σε μια εξαναγκασμένη ταλάντωση
Tags:
Φυσική