Μαθηματικός Πάπυρος της Μόσχας

Ο Μαθηματικός Πάπυρος της Μόσχας είναι ένας αρχαίος Αιγυπτιακός μαθηματικός πάπυρος, που επίσης είναι γνωστός ως «Ο Μαθηματικός Πάπυρος του Γκολενίστσεφ»

από τον πρώτο ιδιοκτήτη του, αιγυπτιολόγο Βλαντιμίρ Γκολενίστσεφ. Ο Γκολενίστσεφ αγόρασε τον πάπυρο το 1892 ή το 1983 στις Θήβες. Κατόπιν έγινε μέρος της συλλογής του Κρατικού Μουσείο Καλών Τεχνών Πούσκιν στην Μόσχα, όπου και παραμένει σήμερα.

Βάσει της παλαιογραφικής ανάλυσης και της ορθογραφίας της ιερατικής γραφής του κειμένου, το πιθανότερο είναι ότι αυτό γράφτηκε κατά την 13η Δυναστεία, γύρω στο 1850 π.Χ., και είναι βασισμένο σε παλιότερο υλικό από την 12η Δυναστεία^[1]. Έχει περίπου $5,5$ μέτρα μήκος και πλάτος μεταξύ $3,8$ με $7,6$ εκατοστά. Το περιεχόμενό του χωρίστηκε σε $25$ προβλήματα με λύσεις από τον Σοβιετικό ασιανολόγο Βασίλι Στρούβε^[2] το 1930.^[3]. Ο Πάπυρος της Μόσχας είναι γνωστός μαθηματικός πάπυρος μαζί με τον Μαθηματικό πάπυρο του Ράιντ, με τον πρώτο να είναι ο παλιότερος, και τον δεύτερο ο μεγαλύτερος από τους δύο^[4].

ΑΣΚΗΣΕΙΣ ΤΟΥ ΠΑΠΥΡΟΥ ΤΗΣ ΜΟΣΧΑΣ

Τα προβλήματα στον πάπυρο της Μόσχας δεν ακολουθούν συγκεκριμένη σειρά, και οι λύσεις περιέχουν λιγότερες λεπτομέρειες σε σύγκριση με τον πάπυρο του Ράιντ. Ο πάπυρος είναι γνωστός για μερικά από τα γεωμετρικά του προβλήματα. Τα προβλήματα 10 και 14 υπολογίζουν τον εμβαδόν μιας επιφάνειας και τον όγκου ενός κόλουρου (ο κύβος ενδεικτικά) αντίστοιχα. Τα υπόλοιπα προβλήματα είναι λίγο πολύ κοινά^[1].

Προβλήματα με μήκος μερών πλοίου

Τα προβλήματα 2 και 3 υπολογίζουν το μήκος μερών πλοίου. Το ένα υπολογίζει το μήκος του πηδαλίου, και το άλλο του καταρτιού του πλοίου δεδομένου ότι είναι το $1/3+1/5$ του μήκους μιας σανίδας κέδρου με μήκος $30$ πήχεις^[1].

Προβλήματα Aha

Aha σε ιερογλυφικά

Τα προβλήματα Aha αφορούν στην εύρεση άγνωστης ποσότητας (που ονομάζεται Aha, - αντίστοιχο του αγνώστου χ) αν δίνεται το σύνολο της ποσότητας και μέρους (ή μερών) του. Ο πάπυρος του Ράιντ επίσης περιέχει τέσσερα τέτοια προβλήματα. Στο πάπυρο της Μόσχας τα προβλήματα $1,19,$ και $25$ είναι προβλήματα Aha. Για παράδειγμα, το πρόβλημα 19 ζητά την ποσότητα που αν έχουμε ένα και ένα δεύτερο ( $1{\tfrac {1}{2}}$ ^[5]) αυτής και προσθέσουμε τέσσερα, θα πάρουμε δέκα^[1]. Δηλαδή με σύγχρονο μαθηματικό συμβολισμό, μας ζητείται να λύσουμε τη πρωτοβάθμια εξίσωση ${\tfrac {3}{2}}\cdot x+4=10$ .

Προβλήματα pefsu

Τα περισσότερα προβλήματα στον πάπυρο (δέκα στα εικοσιπέντε) είναι προβλήματα τύπου pefsu. Το pefsu μετράει πόσο δυνατή είναι η μπύρα που γίνεται από ένα heqat σιτάρι (ή hekat, μονάδα όγκου των αρχαίων Αιγυπτίων που αντιστοιχεί σε $4,8$ λίτρα)

{\text{1 pefsu}}={\frac {\#{\text{(καρβελι}}{\acute {\omega }}{\text{ν)   }}{\acute {\eta }}{\text{   }}\#{\text{(κανατι}}{\acute {\omega }}{\text{ν }}{\text{μπ}}{\acute {\upsilon }}{\text{ρας)}}}{\#({\text{heqat σιταριο}}{\acute {\upsilon }})}}

^{[σ 1]}

Όσο περισσότερα pefsu έχει μια μπύρα, τόσο πιο αδύναμη είναι^{[σ 2]}. Τα νούμερα pefsu αναφέρονται σε πολλές λίστες προσφορών. Για παράδειγμα, το πρόβλημα 8 μεταφράζεται ως εξής:

(1) Παράδειγμα υπολογισμού για

100

καρβέλια ψωμί pefsu

20

(2) Αν κάποιος σου πει: «Έχεις

100

καρβέλια ψωμί pefsu

20

(3) για να τα αλλάξεις με μπύρα pefsu

4

(4) του είδους μπύρας

1/2

κ'

1/4

.» (πόση μπύρα πρέπει να πάρεις;)

(5) Πρώτα υπολόγισε το σιτάρι που χρειάζεται για να φτιάξεις

100

καρβέλια ψωμί pefsu

20

(6) Το αποτέλεσμα είναι

5

heqat. Μετά σκέψου πόσο θέλεις για ένα des-κανάτι μπύρας του είδους

1/2

κ'

1/4

(7) Το αποτέλεσμα είναι

1/2

του heqat για ένα des-κανάτι μπύρας φτιαγμένης με στάρι από την Άνω Αιγύπτου.

(8) Υπολόγισε

1/2

των

5

heqat, το αποτέλεσμα είναι

2{\tfrac {1}{2}}

(9) Πάρε αυτό το

2{\tfrac {1}{2}}

επί

4

φορές

(10) Το αποτέλεσμα είναι

10

. Μετά του λες:

(11) «Ιδού!» Η ποσότητα της μπύρας βρέθηκε και είναι σωστή^[1]^{[σ 3]}.

Προβλήματα baku

Το 11 και το 23 είναι προβλήματα τύπου baku. Αυτά υπολογίζουν την απόδοση εργατών. Το πρόβλημα 11 για παράδειγμα, ρωτάει αν κάποιος κατασκευάζει $100$ σανίδες $5$ επί $5$ τότε πόσες σανίδες $4$ επι $4$ μπορεί να κατασκευάσει. Το πρόβλημα 23 αφορά τον υπολογισμό της απόδοσης ενός υποδηματοποιού και ρωτά, «Όταν ένας υποδηματοποιός φτιάχνει μόνο σαντάλια, φτιάχνει δέκα (10) την ημέρα. Όταν μόνο διακοσμεί (φτιαγμένα) σαντάλια, διακοσμεί πέντε (5) την ημέρα. Πόσα μπορεί να φτιάξει και να διακοσμήσει την ίδια ημέρα;»^[1]^{[σ 4]}.

Προβλήματα γεωμετρίας

Επτά από τα 25 προβλήματα είναι προβλήματα γεωμετρίας, μεταξύ των οποίων ο υπολογισμός του εμβαδού τριγώνων, εμβαδού ημισφαιρίου (πρόβλημα 10), και ο υπολογισμός κόλουρου (κόλουρης πυραμίδας)^[1].

ΔΥΟ ΕΝΔΙΑΦΕΡΟΝΤΑ ΠΡΟΒΛΗΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ

Πρόβλημα 10

Το δέκατο (10ο) πρόβλημα του παπύρου ζητά τον υπολογισμό του εμβαδού ημισφαιρίου (σύμφωνα με τους Στρούβε και Gillings), ή ίσως το εμβαδόν ημί-κυλίνδρου (σύμφωνα με τον Peet). Παρακάτω υποθέτουμε ότι είναι για ημισφαίριο.

Το κείμενο του 10ου προβλήματος αφορά έναν υπολογισμό των διαστάσεων ενός καλαθιού:«Έχουμε ένα καλάθι του οποίου το στόμιο έχει μήκος $4{\tfrac {1}{2}}$ . Ποιο είναι το εμβαδόν του; Πάρε $1/9$ του $9$ (αφού) το καλάθι είναι το μισό σφαίρας. Δίνει μονάδα. Υπολόγισε το υπόλοιπο, είναι $8$ . Υπολόγισε το $1/9$ του $8$ . Δίνει $2/3+1/6+1/18$ . Βρες το υπόλοιπο αυτού το $8$ μετά την αφαίρεση απ’ αυτό του $2/3+1/6+1/18$ . Δίνει $7{\tfrac {1}{9}}$ . Πολλαπλασίασε το $7{\tfrac {1}{9}}$ επί $4{\tfrac {1}{2}}$ . Δίνει $32$ . Ιδού, αυτό είναι το εμβαδόν. Βρήκες ότι είναι σωστό.» ^[1]^[6]

Η λύση ισοδυναμεί με τον υπολογισμό:

{\text{Εμβαδ}}{\acute {o}}=2\times \left({\frac {8}{9}}\right)^{2}\times ({\text{δι}}{\acute {a}}{\text{μετρος}})^{2}=2\times \left({\frac {16}{9}}\right)^{2}\times ({\text{ακτ}}{\acute {\iota }}{\text{να}})^{2}=2\times {\frac {256}{81}}\times ({\text{ακτ}}{\acute {\iota }}{\text{να}})^{2}

Αυτό σημαίνει ότι αυτός που έγραψε τον Πάπυρο της Μόσχας χρησιμοποίησε τον ρητό αριθμό ${\frac {256}{81}}\approx 3.16049$ για να προσεγγίσει την τιμή της μαθηματικής σταθεράς $\pi$ .

Πρόβλημα 14: Όγκος κόλουρης πυραμίδας με τετράγωνη βάση

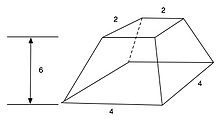
Στο 14ο πρόβλημα υπολογίζεται ο όγκος κόλουρου (κόλουρης πυραμίδας στην στην περίπτωσή μας).

Το πρόβλημα δίνει τα δεδομένα ότι η πυραμίδα έχει γίνει κόλουρη ώστε η πάνω επιφάνεια είναι τετράγωνο με μήκος πλευράς $2$ , η κάτω επιφάνεια τετράγωνο με μήκος πλευράς $4$ , και με ύψος $6$ , όπως φαίνεται στο σχήμα. Ο όγκος υπολογίζεται σε $56$ κυβικούς πήχεις, το οποίο είναι σωστό^[1].

Η εκφώνηση είναι η ακόλουθη: «Σας λένε ότι μια κόλουρη πυραμίδα έχει ύψος $6$ , μήκος $4$ στη βάση και $2$ στην κορυφή. Υψώνετε το $4$ στο τετράγωνο, αποτέλεσμα $16$ . Διπλασιάζετε το $4$ αποτέλεσμα $8$ . Υψώνετε στο τετράγωνο αυτό το $2$ , αποτέλεσμα $4$ . Προσθέτετε το $16$ και το $8$ και το $4$ , αποτέλεσμα $28$ . Παίρνετε το $1/3$ του $6$ , αποτέλεσμα $2$ . Παίρνετε το $28$ δύο φορές, αποτέλεσμα $56$ . Βλέπετε, είναι $56$ . Θα βρείτε ότι είναι σωστό»^[7]. Η λύση του προβλήματος υποδηλώνει ότι οι Αιγύπτιοι γνώριζαν πώς να υπολογίσουν τον τύπο που δίνει τον όγκο κόλουρης πυραμίδας:

V={\frac {1}{3}}h(a^{2}+ab+b^{2}).

Βιβλιογραφία

Allen, Don. April 2001. The Moscow Papyrus and Summary of Egyptian Mathematics.
Imhausen, A., Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden 2003.
Mathpages.com. The Prismoidal Formula.
O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri.
Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: Ancient Egypt and The Moscow Mathematical Papyrus.
Williams, Scott W. Mathematicians of the African Diaspora, containing a page on Egyptian Mathematics Papyri.
Zahrt, Kim R. W. Thoughts on Ancient Egyptian Mathematics.

ΠΗΓΗ

Μαθηματικός Πάπυρος της Μόσχας

ΑΣΚΗΣΕΙΣ ΤΟΥ ΠΑΠΥΡΟΥ ΤΗΣ ΜΟΣΧΑΣ

Προβλήματα με μήκος μερών πλοίου

Προβλήματα Aha

Προβλήματα pefsu

Προβλήματα baku

Προβλήματα γεωμετρίας

ΔΥΟ ΕΝΔΙΑΦΕΡΟΝΤΑ ΠΡΟΒΛΗΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ

Πρόβλημα 10

Πρόβλημα 14: Όγκος κόλουρης πυραμίδας με τετράγωνη βάση

Βιβλιογραφία

Δημοσίευση σχολίου

Φόρμα επικοινωνίας