Όταν γνωρίζουμε τα πολλά και ψάχνουμε το ένα, κάνουμε διαίρεση.
Διαίρεση σημαίνει διαιρώ, δηλαδή μοιράζω, χωρίζω.
Είναι η αντίστροφη πράξη από τον πολλαπλασιασμό : στον πολλαπλασιασμό ξέρουμε το ένα και ψάχνουμε τα πολλά.
Η διαίρεση συνδυάζει όλες τις άλλες πράξεις , την πρόσθεση, την αφαίρεση και τον πολλαπλασιασμό.
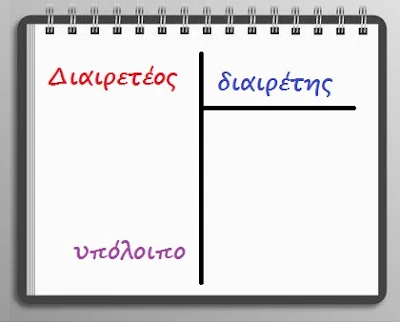
Ο πρώτος αριθμός αριστερά λέγεται Διαιρετέος (Δ)
είναι ο αριθμός που θα μοιραστεί
Ο δεύτερος αριθμός δεξιά ονομάζεται διαιρέτης (δ)
είναι ο αριθμός που θα μοιράσει τον διαιρετέο
Το αποτέλεσμα που βρίσκουμε λέγεται πηλίκο (π)
είναι ο αριθμός που μας λέει πόσες φορές χωράει ο διαιρέτης στον διαιρετέο
Αυτό που περισσεύει (αν υπάρχει) λέγεται υπόλοιπο (υ)
Η διαίρεση βήμα βήμα
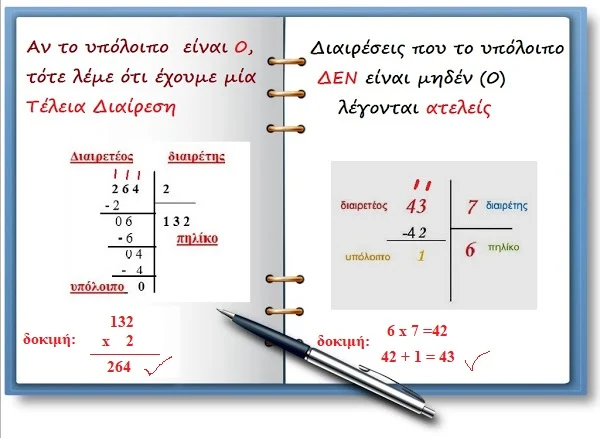
Ένα ψηφίο έχει ο διαιρέτης κι ένα χωρίζουμε από τα αριστερά του Διαιρετέου (πάνω από το 2 βάζουμε έναν τόνο)
Το 2 στο 2 χωράει 1 φορά.
Γράφουμε το 1 στο πηλίκο και το πολλαπλασιάζουμε με τον διαιρέτη: 1 x 2 = 2.
Το 2 το γράφουμε κάτω από το 2 και το αφαιρούμε. 2 – 2 = 0
Δίπλα στο 0 κατεβάζουμε το δεύτερο ψηφίο του διαιρετέου, το 6 (και το σημειώνουμε με έναν τόνο).
Το 2 στο 6 χωράει 3 φορές.
Γράφουμε το 3 στο πηλίκο και το πολλαπλασιάζουμε με τον διαιρέτη 3 x 2 = 6. Γράφουμε το 6 κάτω από το 6 και το αφαιρούμε.
6 - 6 = 0
Δίπλα στο 0 κατεβάζουμε το τρίτο ψηφίο του διαιρετέου το 4 (και το σημειώνουμε με έναν τόνο).
Το 2 στο 4 χωράει 2 φορές.
Γράφουμε το 2 στο πηλίκο και το πολλαπλασιάζουμε με τον διαιρέτη 2 x 2 = 4.
Το γράφουμε κάτω από το 4 και το αφαιρούμε.
4 - 4 = 0
άλλη μία διαίρεση...
Ένα ψηφίο έχει ο διαιρέτης κι ένα χωρίζουμε από τα αριστερά του Διαιρετέου (πάνω από το 4 βάζουμε έναν τόνο)
Το 7 στο 4 δε χωράει. Γι΄αυτό τονίζουμε και το δεύτερο ψηφίο, το 3.
Το 7 στο 43 χωράει 6 φορές.
Γράφουμε το 6 στο πηλίκο και το πολλαπλασιάζουμε με τον διαιρέτη 6x7 = 42.
Το γράφουμε κάτω από το 43 και το αφαιρούμε
43 - 42 = 1
Η επαλήθευση της διαίρεσης είναι ο πολλαπλασιασμός :
πολλαπλασιάζουμε τον διαιρέτη με το πηλίκο
και
προσθέτουμε το υπόλοιπο (αν υπάρχει).
Αν βρούμε από τον πολλαπλασιασμό τους τον Διαιρετέο, τότε η διαίρεση που κάναμε είναι σωστή
Tags:
Μαθηματικά